CRC-Berechnung
In diversen U880-Programmen, z.B. EPROM-Software, wird oftmals eine Prüfsumme ausgegeben. Dabei handelt es sich fast immer um eine 16 BIT-CRC-Prüfsumme, d.h. ein 17-Bit-Polynom, nach Standard CCITT:
CRC-CCITT (CRC-16) x^16 + x^12 + x^5 + 1
s. Wikipedia
Als Startwert wird eigentlich immer 0FFFFh genommen.
In der DDR-Literatur liest man auch oft „SDLC-Polynom“. SLDC (Synchronous Data Link Control) wurde Mitte der 70er von IBM für die Kommunikation zwischen ihren Rechnern über die System Network Architecture (SNA) entwickelt. Als Standard-CRC kommt hier das obige CRC16-CCITT-Polynom zum Einsatz.
In Perl kann man die CRC so berechnen (nicht optimiert, reine Umsetzung des Polynoms!). Die Und-Verknüpfung mit 0x8000 erfolgt zur Maskierung des Hi-Bits 15; Die Und-Verknüpfung mit 0xFFFF ist nötig, um das Ergebnis als 16Bit-Zahl zu belassen.
$buf = ....; #Arrays von 2KiByte FFh $len = 2048; #Anzahl der Bytes #CRC-CCITT (CRC-16) x16 + x12 + x5 + 1 $POLY = 0b_0001_0000_0010_0001; # das 17. Bit (x^16) entfällt, # da nur mit 16 Bit gearbeitet wird #Startwert $crc16 = 0xFFFF; for ($i=0;$i<$len;$i++) { my $byte = ord(substr($buf,$i,1)); # nächstes Byte aus Buffer holen $byte = $byte * 0x100; # in 16 Bit wandeln for (0..7) # 8 Bits pro Byte { if (($byte & 0x8000) ^ ($crc16 & 0x8000)) { # wenn die Hi-Bits unterschiedlich sind, dann $crc16 <<= 1; # shift left $crc16 ^= $POLY; # XOR-Verknüpfung mit CRC-Poly $crc16 &= 0xFFFF; # beschränken auf 16 Bit } else { # ansonsten nächstes Bit ohne Verküpfung $crc16 <<= 1; # shift left $crc16 &= 0xFFFF; # beschränken auf 16 Bit } $byte <<= 1; # shift left, nächstes Bit $byte &= 0xFFFF; } } # Ausgabe printf "CRC = %.4X\n", $crc16;
Normalerweise werden CRC-Polynome mit reverser Bit-Reihenfolge berechnet; auch die einzelnen Bytes werden in umgekehrter Reihenfolge abgearbeitet. Und richtig optimal wird es erst mit vorbrechneten Tabellen…
In Assembler sieht die CRC-Routine wie folgt aus. Die Berechnung ist optimiert und erfolgt tetradenweise. (Der Code stammt aus der Z9001-EPROM-Software)
in: DE = Startadr., BC = Länge
out: HL = CRC
;------------------------------------------------------------------------------ ; CRC berechnen ; Routine aus EPROMA2 ; in DE = Startadr., BC = Länge, out HL=CRC ; CRC-CCITT (CRC-16) x16 + x12 + x5 + 1 ;------------------------------------------------------------------------------ crc: ld hl, 0FFFFh crc1: ld a, (de) xor h ld h, a rrca rrca rrca rrca and 0Fh xor h ld h, a rrca rrca rrca push af and 1Fh xor l ld l, a pop af push af rrca and 0F0h xor l ld l, a pop af and 0E0h xor h ld h, l ld l, a inc de dec bc ld a, b or c jr nz, crc1 ret
und hier eine direkte Implementierung ohne Optimierung (und dadurch langsamer, aber leichter zu verstehen)
;------------------------------------------------------------------------------ ; CRC berechnen ; Routine aus FA 11/86 ; ab HL, bis DE, ret HL=CRC (SDLC x16+x12+x5+x1) ;------------------------------------------------------------------------------ ; ab DE, BC Bytes, ret HL=CRC crc_fa0 ld h,d ld l,e dec bc add hl,bc ex hl,de ld (arg2),de ; ab HL, bis (arg2), ret HL=CRC crc_fa ld de, 0FFFFh ; rücksetzen CRC bytecrc ld b,80h ; beginne mit Bit 7 crclp1 sla e ; CRC schieben rl d sbc a,a ; Cy=1 -> A=FF xor (hl) ; Cy=0 -> A=00 and b jr z,crc0 ;Rückkopplung CRC-Generator ld a,e xor 21h ; 0010_0001 bei SDLC ld e,a ld a,d xor 10h ; 0001_0000 bei SDLC ld d,a crc0 srl b jr nc,crclp1 ; Byte fertig? ; ld bc,(arg2) xor a ; Cy -> 0 sbc hl,bc add hl,bc inc hl jr nz,bytecrc ; fertig? ex de,hl ; CRC nach HL ret arg2 ds 2 end
s.a.
- http://www.ac1-info.de/literatur/fa_86_11.htm (Berechnung nach SDLC, mit Bit-Schieberegister)
Hardware
aus mc 1984/07
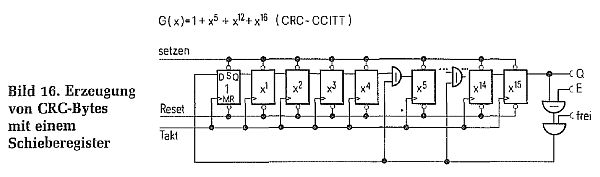
CRC ist die Abkürzung für Cyclic Redundancy Check und so etwas ähnliches wie eine Prüfsumme, darf aber damit nicht verwechselt werden, da die Erzeugung des CRC aufwendiger ist. Dabei werden nicht einfach die einzelnen Bytes aufaddiert, sondern verschiedene Bits gemäß einem sogenannten Generator- Polynom. Es gibt dabei sehr unterschiedliche Vorschriften, jedoch verwendet man bei den gängigen Controllern das vom CCITT definierte Polynom. Es lautet G(x) = 1 + x^5 + x^12 + x^16. Daraus kann man eine Schaltung konstruieren, die etwa wie in Bild 16 aussieht. Ein Reset-Eingang sorgt dafür, daß das Schieberegister auf einen definierten Wert gesetzt werden kann. Dann werden der Eingang FREI auf 1 gelegt und zusammen mit einem Takt die Daten an E angelegt. Nach dem Ende des Datenstroms wird FREI auf 0 gelegt, und die CRC-Bytes können aus dem Register geschoben werden. Um nun einen Datenstrom zu testen, wird genauso wie vorher verfahren, nur daß nun auch die CRC-Bytes mitverrechnet werden. Das Ergebnis im Schieberegister muß anschließend 0 sein.
